Little book of semaphores Ch 4 - Classical Synchronisation Problems

Producer-Consumer

Required constraints:

Buffer should have exclusive access
If a consumer thread comes and the buffer is empty, it waits

# Initialize
mutex = Semaphore(1)
items = Semaphore(0)
 
# Producer
event = waitForEvent()
mutex.wait()
	buffer.add(event)
mutex.signal()
items.signal() # An item is added
 
# Consumer
items.wait() # Claim an item that we'll consume
mutex.wait()
	event = buffer.get()
mutex.signal()
event.process()

Finite Buffer

Now we have a bufferSize which is the max size of the buffer. The producers must block if this max size is reached.

# Initialize
mutex = Semaphore(1)
items = Semaphore(0)
bufferCapacity = Semaphore(bufferSize)
 
# Producer
event = waitForEvent()
bufferCapacity.wait() # Reserve a space in the buffer, block if not available
mutex.wait()
	buffer.add(event)
mutex.signal()
items.signal() # An item is added
 
# Consumer
items.wait() # Claim an item that we'll consume
mutex.wait()
	event = buffer.get()
mutex.signal()
bufferCapacity.signal() # Signal that one more space is available in the buffer
event.process()

Reader-Writer Problem

Constraints

Writer should have exclusive access
Any number of readers can have access simultaneously

# Initialise
readers = 0
mutex = Semaphore(1)
roomEmpty = Semaphore(1)
 
# Reader thread
mutex.wait()
	if readers == 0:
		roomEmpty.wait() # Waiting for a writer thread if present
		# Intentionally not releasing lock
	readers = readers + 1
mutex.signal()
# Do reader stuff
mutex.wait()
	readers = readers - 1
	if readers == 0:
		roomEmpty.signal()
mutex.signal()
 
# Writer thread
roomEmpty.wait()
# Do writer stuff
roomEmpty.signal()

Semaphore naming convention

Here we have named a semaphore as a condition roomEmpty. Calling wait() on it means waiting for the condition to become true and signal() means signalling that the condition is now true

The pattern used in the above code is called Lightswitch, which means that first person in the room turns on the light (locks the mutex) and the last person out turns off the light (unlocks the mutex). The lightswitch related code can be wrapped in a class for clarity

Lightswitch abstraction

class Lightswitch:
	# init sets count = 0 and creates a mutex
	def lock(self, roomEmpty):
		self.mutex.wait()
		if count == 0:
			roomEmpty.wait()
		count = count + 1
		self.mutex.signal()
 
	def unlock(self, roomEmpty):
		self.mutex.wait()
		count = count - 1
		if count == 0:
			self.roomEmpty.signal()
		self.mutex.signal()

Reader Starvation

In the above solution, a writer can starve waiting in the queue while readers come and go. Let’s fix it so when a writer comes no other readers can enter the critical section, only the existing readers are allowed to finish

# initialise
readLightswitch = Lightswitch()
roomEmpty = Semaphore(1)
readerTurnstile = Semaphore(1) # Initially the turnstile is open
 
# Reader thread
readerTurnstile.wait()
readerTurnstile.signal()
readLightswitch.lock(roomEmpty)
# Reader stuff
readLightswitch.unlock(roomEmpty)
 
# Writer thread
readerTurnstile.wait() # Turn off the reader turnstile so no other readers pass
roomEmpty.wait()
# Do writer stuff
roomEmpty.signal()
readerTurnstile.signal() # Turn on the reader turnstile

Writer Priority readers-writers

We want to design a solution where if a writer enters, then no other reader may enter while the writers are queued. This will give priority to writers.

# initialise
readLightswitch = Lightswitch()
writerLightswitch = Lightswitch()
roomEmpty = Semaphore(1)
readerTurnstile = Semaphore(1)
 
# Reader thread
readerTurnstile.wait()
readerTurnstile.signal()
readLightswitch.lock(roomEmpty)
# Reader stuff
readLightswitch.unlock(roomEmpty)
 
# Writer thread
writerLightswitch.lock(readerTurnstile)
roomEmpty.wait()
# Do writer stuff
roomEmpty.signal()
writerLightswitch.unlock(readerTurnstile)

Here, the writer thread is treating the readerTurnstile as a lock. It is locked through the lightswitch pattern allowing writers to enter while there is any writer present. Writers are then serialised through the roomEmpty mutex.

No-starve Mutex

In previous sections, the starvation we talked about is categorical starvation. It’s the category of the problem which causes the starvation. It can come at a more basic level too, where a waiting thread might never run.

Starvation is partly the property of the scheduler. If it never runs a thread that is waiting, then it will starve. So we make assumptions about the scheduler

Property 1

if there is only one thread that is ready to run, the scheduler has to let it run.

Using this property, we can construct a program free of starvation. E.g. a program with a barrier: eventually all but one thread will be at the barrier and then the last thread must run by the above property. However, we usually need a stronger property

Property 2

if a thread is ready to run, then the time it waits until it runs is bounded.

Note that there are schedulers where this property is not present. We will continue to assume it though. Starvation can happen now due to semaphores.

Property 3

if there are threads waiting on a semaphore when a thread executes signal, then one of the waiting threads has to be woken.

This is the weakest property we can have for having starvation-free semaphore code. Without this, we can have a thread signalling and then later calling wait and getting its own signal.

Even with this property, something like a mutex is prone to starvation. Consider the following code run by multiple threads:

while True:
	mutex.wait()
	# Work
	mutex.signal()

Suppose we have threads A, B, C. Thread A is running the critical section and the others at waiting at the wait() call. A’s signal then goes to B which wakes up and enters the critical section. Before it exits, A also joins the queue with C of waiting on the mutex. Then B’s signal can go to A. Continuing that, we can see that C will get starved.

Property 4

if a thread is waiting at a semaphore, then the number of threads that will be woken before it is bounded

A semaphore that has Property 4 is called a strong semaphore while a semaphore having only Property 3 is called a weak semaphore. Dijkstra conjectured it is not possible to have a starvation free mutex with a weak semaphore. It was later refuted by J.M. Morris.

Using weak semaphores

Similar to the reusable barrier solution, we use 2 turnstiles to create 2 waiting rooms:

In the first phase, the first turnstile is open and the second is closed. Threads accumulate in the first waiting room
In the second phase, the first turnstile is closed and the second is open through which threads can get to the critical section. The threads in the second waiting room are bounded and will run the critical section before any future arrivals.

room1 = room2 = 0 # Number of threads in the rooms
mutex = Semaphore(1) # Protect the room1 counter
t1 = Semaphore(1) # turnstile to enter room 1
t2 = Semaphore(0) # turnstile to enter room 2

The solution:

mutex.wait()
	room1 += 1
mutex.signal()
 
t1.wait() # Wait for the first room second room door to open
	room2 += 1
	mutex.wait()
	room1 -= 1
 
	if room1 == 0:
		mutex.signal()
		t2.signal() # Open the second turnstile into the critical section
		# Not opening the first turnstile, so it will stay locked
	else:
		mutex.signal()
		t1.signal() # More threads need to pass into the second room
 
t2.wait() # Wait for the door into critical section
	room2 -= 1
 
	# Critical section
 
	if room2 == 0:
		t1.signal() # Second turnstile will stay closed
	else:
		t2.signal() # Let more waiting room 2 threads pass into crit. section

How does this solution work?

room1 is protected by mutex. It signifies if a thread is waiting in the first waiting room.
In the first phase, when room1 == 0 condition is not hit:
- A thread will go to sleep waiting on t2
- Eventually, room1 == 0 will become true as there are a finite number of threads. When all but one are sleeping on t2, then the one has to be run by Property 1.
When room1 == 0 becomes true:
- t1 will stay locked and t2 will be unlocked
- t2 will ensure exclusive access to the critical section.
How room2 is maintained:
- room2 is modified only while holding t1 or t2. Since t1 and t2 are not simultaneously unlocked ever, only one thread can modify room2 at a time
- room2 will eventually become 0 as there are finite threads in the waiting room, and then the first turnstile will be opened.

Observe that it is very difficult to write starvation-free code using only weak semaphores. In the following sections, we’ll assume strong semaphores.

Dining Philosophers

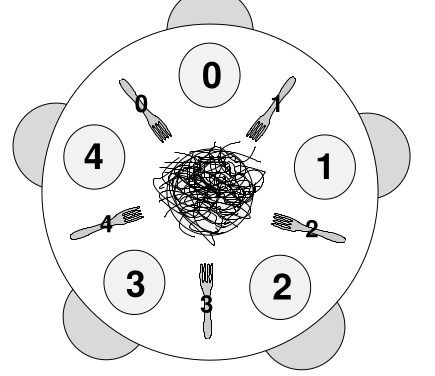There are 5 philosophers and 5 forks. A philosopher needs 2 forks to eat. We have to solve the following:

One fork held by only one guy at a time
Must be impossible for a deadlock
A philosopher should not starve
Should be possible for more than one guy to eat

# Basic Philosopher loop
while True:
	think() # Can take any amount of time
	get_forks()
	eat() # Can take any amount of time
	put_forks()

We have functions left(i) and right(i) which give indices of left and right spoons of the philosopher at position i. We can represent one fork as a semaphore

forks = [Semaphore(1) for i in range(5)]

The normal solution of everyone picking the left fork first and then the right fork results in a deadlock. Let’s try to do better.

My solution

We should acquire the forks in increasing order of index, that fixes the deadlock.

def get_forks(i):
	if left(i) < right(i):
		forks[left(i)].wait()
		forks[right(i)].wait()
	else:
		forks[right[i]].wait()
		forks[left[i]].wait()

put_forks should also release the forks in the same oder

Hint

If there were only 4 philosophers at the table, deadlock is impossible. This is 1 philosopher will be able to get forks by the pigeon hole principle. So we can write code to limit the philosophers on the table. Let’s define a variable can_get_fork = Semaphore(4).

def get_forks(i):
	can_get_fork.wait()
	forks[right[i]].wait()
	forks[left[i]].wait()
 
def put_forks(i):
	forks[left[i]].signal()
	forks[right[i]].signal()
	can_get_fork.signal()

This solution also has the benefit that no philosopher will starve. One philosopher is waiting at the can_get_fork semaphore, and eventually it will be woken up as we’re assuming a strong semaphore. Similarly, other philosophers waiting on forks will also be woken up. Both of these hinge on the fact that time taken by eat() is bounded.

Leftie Rightie

If there is at least one leftie (person which picks the left fork first) and one rightie on the table, then deadlock is not possible

Why is that?

Deadlock is only possible when all philosophers are holding a fork in their one hand and spoon on their other side is held by someone else. Otherwise, 1 philosopher will be able to eat and then leave both the forks
The above situation is only possible when all the philosophers are holding forks in their same side hand. If atleast one holds their fork in a different hand first, this cannot happen

Arpit Saxena

Little book of semaphores Ch 4 - Classical Synchronisation Problems

Table of Contents

Producer-Consumer

Finite Buffer

Reader-Writer Problem

Lightswitch abstraction

Reader Starvation

Writer Priority readers-writers

No-starve Mutex

Using weak semaphores

Dining Philosophers

My solution

Hint

Backlinks

Graph View

Table of Contents